The mathematics of unstable systems
What is chaos theory?
Have you thought about why weather predictions are inaccurate more than a couple of days in advance? Most complex systems in nature are highly sensitive to 'initial conditions,' meaning a small change in how the system is set up leads to large differences later. This is Chaos theory, an important branch of mathematics. It includes systems as simple as a double pendulum and as complex as a tornado, and involves contributions from scientists from all over the world.
A brief history of chaos
James Clerk Maxwell (a Scot who worked here at King’s College London) was one of the first researchers to study chaotic systems and the "butterfly effect." In France, Henri Poincaré discovered chaos in a very simple system: just three bodies interacting gravitationally, the famous three-body problem. A system with two masses can be solved exactly, but three masses means that a very small change in their initial positions or velocities leads to wildly different paths.
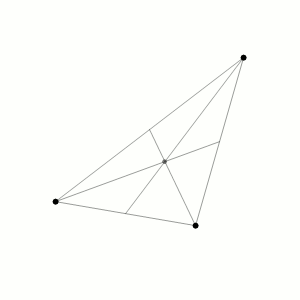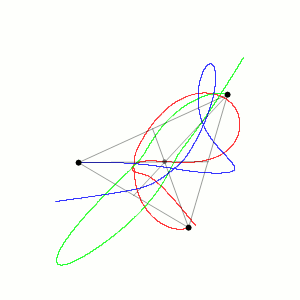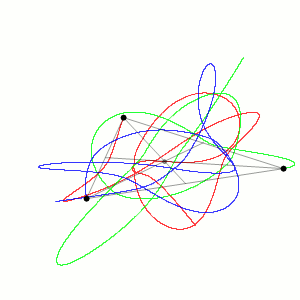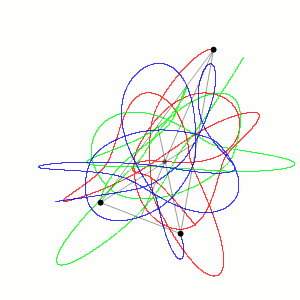
American mathematician Edward Lorenz and his collaborators Ellen Fetter and Margaret Hamilton were studying weather patterns in the 1960s using an early computer. They were trying to run a simulation again from the middle point using printout data. But they were surprised to discover that inputting what seemed as the same values was giving different patterns! The difference was that the computer worked with 6-digit precision, but the printout rounded variables off to a 3-digit number, so a value like 0.698132 printed as 0.698. This tiny difference produced big changes in the long run, this is what makes long-term weather prediction impossible.
 |
 |
 |
Lorenz is also famous for his study of the “Lorenz system”. This is a system of equations that can be a model for the weather but also systems such as circuits and motors. When the trajectories, the paths in space are plotted, they often resemble the wings of a butterfly. The Lorentz system is a famous chaotic system, a very small change in the initial conditions leads to very different trajectories.
 |
 |
Is the pendulum in a clock chaotic? Why or why not?
The pendulum in a clock is not a chaotic system. The pendulum in a clock is a very predictable system, and it needs to be to keep time!
The Brazilian school of chaos
Mauricio Peixoto was one of the most famous Brazilian mathematicians. In the 1950’s he proved his famous Peixoto theorem: most systems which require only two numbers to specify their state are not chaotic.
Stephen Smale is an American mathematician, famous for his studies in chaos theory. When he visited Peixoto in Brazil he made an important discovery regarding the "horseshoe map". What is a horseshoe map? Imagine that you have a square. Now you stretch it, bend it and place it into another square the same size as the original one, like a horseshoe (see image). Now repeat the process.
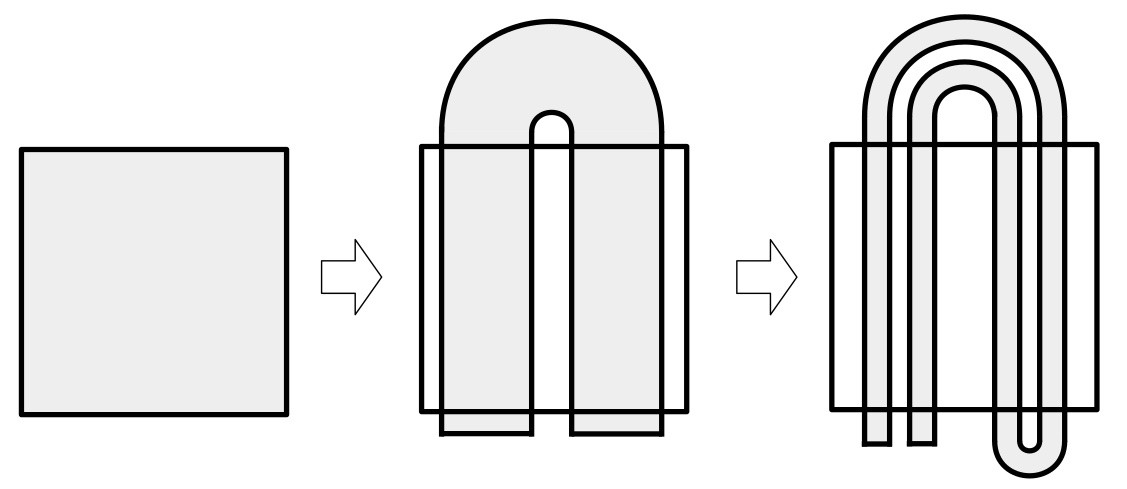
If you pick a point in the original square, it will move around at every horseshoe folding. Smale proved however that there is an infinite set of points that always remain in the original square. Chaos is contained in this case!
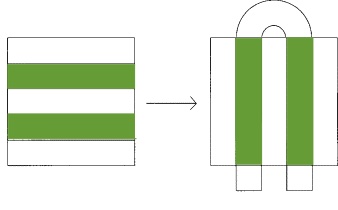
If a point in the original square winds up in the square after a folding, it should lie in one of the two horizontal strips shown. Can you think why?

The Brazilian school had a great impact on the development of Dynamical Systems and Chaos as many mathematicians working on chaos lived and studied there.
Chaos in nature
Chaotic systems appear in every science: biology, geology, economics, robotics, even politics! They are particularly prevalent in nature. For example population dynamics in many species are often chaotic; like weather, they cannot be predicted in the long term.

But chaos can also be found in the patterns on animal species such as stripes and spots. English mathematician Alan Turing studied this process and showed that when two specific substances interact with each other an almost periodic pattern forms even from a random or almost uniform initial condition.
Turing's work as a codebreaker played a major role in the defeat of Nazi Germany in second world war, but was subsquently persecuted in the 1950’s as he was gay. You can find out more about Turing's life on our page "Does it matter who made mathematics?".
Can you think of any other chaotic systems in nature?



