Tiling the plane

Can you imagine the infinite?

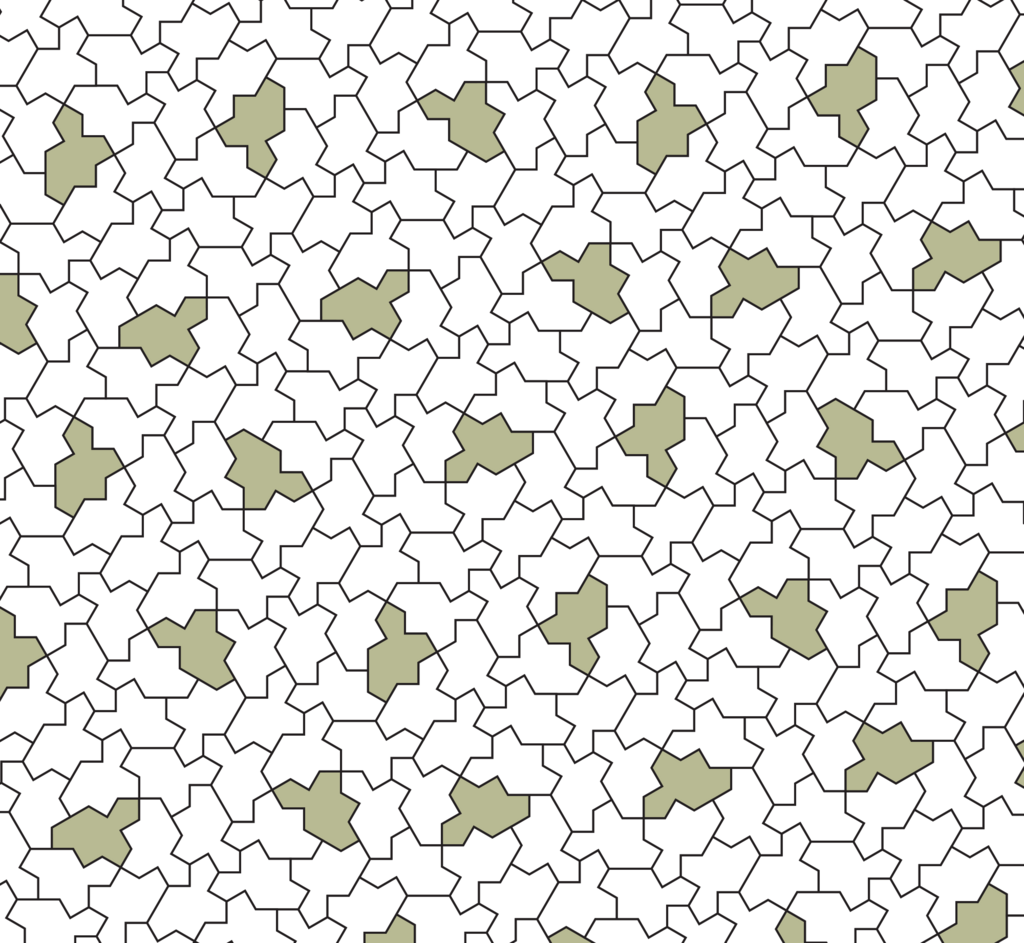
In 2022 the mathematician David Smith discovered that it was possible to tile an the infinite plane with a single special tile, but it is only possible with a pattern that never repeats. This tile is called an einstein tile from the German ein meaning "one" and stein meaning "stone".

Einstein Tiling - By David Smith, Joseph Samuel Myers, Craig S. Kaplan, and Chaim Goodman-Strauss, 2023

David Smith is an amateur mathematician who lives in Bridlngton, Yorkshire.

The problem of finding an einstein tile had been on mathematicians minds since the 1960s when a number of similar never-repeating pattern were found, but which required at least two tiles. Robert Berger found the first tiling, but he needed 20,426 tiles.

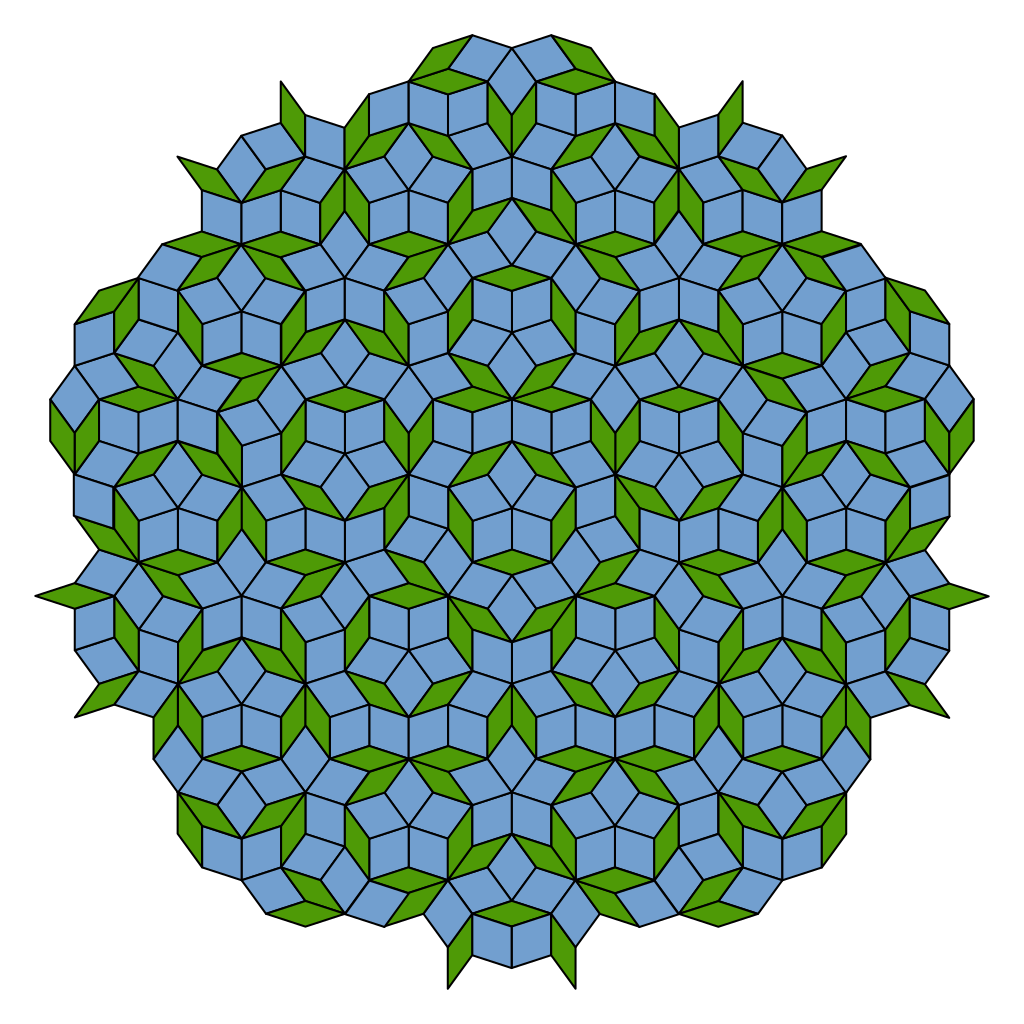
For a long time, the closest we had got to finding the Einstein was the Penrose Tiling which needs two tiles, shown in green and blue. It was found by British mathematician Roger Penrose in 1974.

Part of a Penrose Tiling

QUESTION:

Can you come up with a repeating tiling of the infinite plain using a symmetrical right-angle triangle? Can you come up with a way that of doing this that never repeats?

It isn't too hard to solve this question.

What is magical about an einstein is not just that you can tile the plane in a non-repeating pattern, but also that you can't use it to tile the plane with a repeating pattern.

Islamic Art

Very similar tiling patterns to the Penrose Tiling have been found in Islamic art, for example in the Darb-i Imam shrine built in 1453.

Tiling at the Darb-i Imam shrine. Image: K. Dudley and M. Elliff

The beautiful feature that these tilings share with the Penrose tiling is their five-fold symmetry. This is impossible to achieve with repeating patterns of tiles.

The concept of the infinite plane is crucial in traditional Islamic Art. In Islam, God is abstract and may not be visualised. Filling space with tessellating shapes symbolically conveys the infinite nature of God, but no human mind can comprehend the true vastness of God. Infinite never-ending patterns bring to mind the creator of the universe in a way that is non-representational.

Seventeen types of symmetry

Mathematicians have classified all the possible regular patterns you can use to tile the plane according to their symmetries. You can change the details of the pattern painted on a tile, but only seventeen fundamentally different types of symmetry are possible. Five-fold symmetry is impossible in repeating patterns.

Mathematicians have proved similar results for the symmetries of atoms in crystals. This tells us what possible crystals can form in nature. Materials scientist Dan Shechtman discovered that it is possible to create quasicrystals which have non-repeating patterns similar to Penrose tilings with seemingly impossible five-fold symmetry. He won the Nobel Prize in Chemistry in 2011 for this discovery.

Because there are only seventeen fundamentally different patterns, they can be found in art across the world. The Alhambra palace in Spain contains many of these patterns, and arguably all seventeen. People debate the point as the symmetry of a pattern depends on whether you take the colour into account.

The table below lists all seventeen different patterns and describes their symmetries in words. A "glide reflection" is a symmetry of a wallpaper pattern where you first reflect the pattern and then make a shift along the axis of reflection.

Example	Where	Symmetries
	Medieval Europe	No rotations or reflections.
	Hawaian Cloth	180 degree rotations around two points.
	Egyptian Tomb	Reflections in parallel axes. No rotations.
	Pavement, Austria	Glide reflections in parallel axes. No rotations.
	Alhambra, Spain	Reflections in parallel axes and a glide reflection. No rotations.
	Mummy case	Reflections in perpendicular axes and 180 degree rotations about four points.
	Hawaian cloth	Reflections in parallel with glide reflection perpendicular to reflections. 180 degree rotations about two points. Rotations centered on glide reflection axes.
	Bronze vessel, Assyria	Glide reflections in perpendicular directions. 180 degree rotations about two points, not centered on glide reflection axes.
	Egyptian tomb	Reflections in perpendicular directions. A 180 degree rotations about a point not on a reflection axis and two rotations centred on reflection axis.
	Egyptian tomb	Two rotations of 90 degrees, one of 180 degrees. No reflections.
	Egyptian tomb	Two rotations of 90 degrees. Four reflections in four distinct directions. Four rotations of 180 degrees (on midpoints of squares). Two perpendicular glide reflections on (axes connecting adjacent midpoints).
	Porcelain, China	Two rotations of 90 degrees. Reflections in two distinct directions. Two rotations of 180 degrees about intersection of reflection axes. Glide reflections both parallel to reflections and at 45 degrees.
	Pavement, Poland	Three rotation centres of 120 degrees. No reflections or glide reflections.
	Persian Tile	Three rotation centres of 120 degrees. Reflections in the three sides of an equilateral triangle. The centre of every rotation lies on a reflection axis. Glide reflections in three directions.
	Painting China	Three rotation centres of 120 degrees including a rotation which does not lie on a reflection axis. Reflections in the three distinct directions. Glide reflections in three directions.
	Alhambra, Spain	One 60 degree rotation, two 120 degree rotations, three 180 degree rotations. No reflections or glide reflections.
	Persian tile	One 60 degree rotation, two 120 degree rotation, and three 180 degree rotations. Reflections in six distinct directions. Glide reflections in six distinct directions.