Eratosthenes, Madhava and Ramanujan

What, precisely, is the value of pi?

How can you compute the number pi (π) as accurately as possible? π is defined to be the the ratio of the circumference to its diameter, so one idea might be to draw a very large circle and measure its circumference and its diameter.

One very large circle is the equator. Any circle going all the way round the earth is called a "great circle". One of these is the equator, but there are also great circles going through the north and south pole and all great circles have the same length.

The Greek mathematician Eratosthenes worked out how to mesaure the circumference of these great circles by measuring shadows. Suppose that on one day of the year in some location B, the sun is directly overhead so that nothing casts a shadow. Suppose that at another point A, a vertical pillar casts a shadow so that the line from the top of the pillar to the tip of the shadow is at an angle $\theta$.

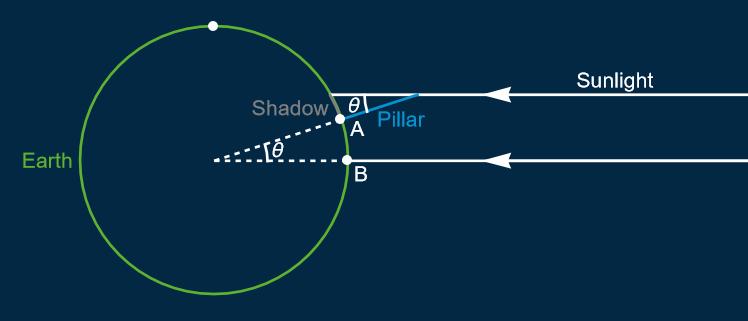
You can work out what proportion of the great circle lies between A and B by dividing θ by 360 degrees. This means that if you know the length of the curve from A to B and you know θ you can work out the circumference of the great circle.

Were the Ancient Greeks Greek?

The Ancient Greek empire was larger than modern Greece and included parts of North Africa. The city of Alexandria in modern day Egypt was at the heart of Alexandria. Without the printing press, books were precious and scholars were attracted to Alexandria by its great library.

Eratosthenes was born in Cyrene which is in modern day Libya. So as well as being an Ancient Greek, Eratosthenes was African. His measurement of the earth all took place in Africa.

Madhava of Sangramama

Unfortunately, knowing the circumference of the earth isn't much help in calculating the value of pi as we can't drill through the earth to measure its diameter!

But Eratosthenes idea can be used to calculate pi as accurately as you like using just maths. You don't need measure anything at all!

Try out our challenge "How do you calculate the length of a curve?" to see how it is done.

Over the centuries, mathematicians have come up with some amazing formulas which you can use to calculate pi. The most beautiful one was discovered by the Indian mathematician Mahava of Sangramama in Kerala (or, perhaps, by one of his followers). This is his formula:

$$\frac{\pi}{4}=1 - \frac{1}{3} + \frac{1}{5} - \frac{1}{7} + \frac{1}{9} - \frac{1}{11} + \ldots $$

The "..." indicate that the formula on the right-hand side goes on forever! You cannot actually add an infinite number of terms. What this is saying is that you can approximate $\frac{\pi}{4}$ using any the first, say, one million terms on the right-hand side. The more terms you use, the more accurate the approximation and you can make the approximation as accurate as you want by using enough terms.

Madhava was the first person to discover this amazing formula. To prove it you need to know a little more maths than is taught at GCSE. The easiest way to prove it is to use a method called calculus which is taught at A-level in the UK. Two European mathematicians, Gregory and Leibniz (from Germany in 1673) indepedently rediscovered the same formula centuries after Madhava.

We don't know exactly when Madhava discovered the formula but it was in the 14th or 15th century. Gregory discovered it in 1671 in Scotland, Leibniz discovered it in Germany 1673. Although Europeans had travelled to Kerala where Madhava lived, there is no convincing evidence that Madhava's discovery influenced Gregory or Leibniz.

The formula is often called "Leibniz's formula" though it is increasingly called the Madhava-Leibniz series. Madhava is still not well-known among mathematicians. Madhava's work was discovered in the west by Charles Whish in 1834, but Whish's work didn't get noticed. Madhava's was rediscovered in the twentieth century and through the work of many, mostly Indian, historians of mathematics it has gradually become better known, but has only begun to be a standard topic in history of mathematics textbooks this century.

Ramanujan

The Indian mathematician Srinivasa Ramanujan came up with another remarkable formula for pi. Madhava's formula is very simple and beautiful, but it is not very good for calculations as you need about one million terms to calculate pi to 5 decimal places. Ramanujan's formula is much more complex, but it gets accurate answers very fast.

This is Ramanujan's formula. Don't worry if you can't understand the equation, it uses maths notation that is not taught at GCSE. Part of the fun of mathematics is realising that, if you put your mind to it, you can learn to understand formulae which look entirely mysterious at first. The maths equations you already understand will have looked incomprehensible to you when you first met them.

$$\frac{1}{\pi} = \frac{2 \sqrt{2}}{99^2} \sum_{k=0}^\infty \frac{(4k)!}{(k!)^4} \frac{26390 k + 1103}{396^4k}$$

While most mathematicians have not heard of Madhava, Ramanujan is very famous among mathematicians and has even had two films made about him: The Man who Knew Infinity and Ramanujan.

One reason that Ramanujan is so famous is that he taught himself mathematics. It is hard enough to come up with big ideas in mathematics even if you have been lucky enough to have the best teachers, so Ramanujan's story is incredible.

World Records

In the 1760s Johann Heinrich Lambert (born in what is now France) proved that the number pi is irrational, which means it cannot be written as a fraction. This implies that its decimal expansion is infinite and non-repeating. We will never know all the digits of pi and so there will always be a world record for computing pi to the largest number of decimal places.

Using modern variations on Ramanujan's formula developed by the Japanese mathematician Sato we can now calculate pi to trillions of decimal places. As of March 13, 2024 the record for calculating pi is 105 trillion digits, computed by Jordan Ranous, Kevin O’Brien and Brian Beeler. The algorithm they use was developed by the Ukrainian mathematicians and engineers David Volfovich Chudnovsky and Gregory Volfovich Chudnovsky in 1989.

We cannot possibly measure the circumference of a circle to an accuracy of trillions of decimal places. Even if you drew a circle as large as the universe and measured its circumference to the accuracy of an atom, you could only measure it to an accuracy of about 33 decimal places. This means that when we calculate pi to trillions of decimal places, we are calculating something about a mathematical model of a circle and not about real circles.

Because everything is made of atoms, you cannot draw a perfect circle. However, some artists can draw amazingly good ones!