Calculating pi without calculus

Challenge: How do you calculate the length of a curve?

This page follows on from Eratosthenes' calculation of the circumference of the world and asks how we can compute pi just using maths. Madhava was able to come up with a way of calculating pi that just uses addition, subtraction and division, but the maths is a quite a bit beyond GCSE. We will come up with a method of calculating pi that works so long as you can calculate square roots.

This page is quite long for a maths calculation using only GCSE maths and uses some notation that will be difficult if you haven't seen it before. Don't worry if it is hard to follow, or if you can't follow it at all! It is here as a deliberate challenge.

As you practice doing maths you can start to understand longer and longer proofs. The trick is to break things down into steps and read a little at a time.

Using Eratosthenes' idea to calculate pi

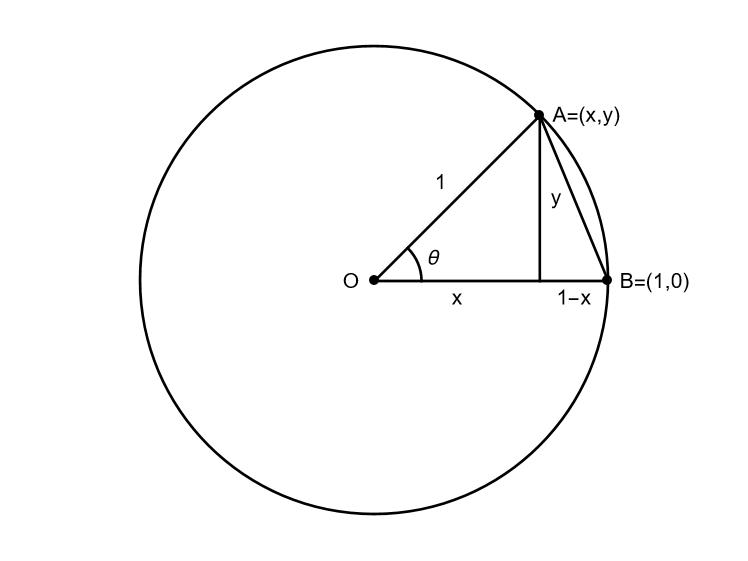
Suppose that a circle has centre O with coordinates (0,0) and radius 1. Suppose that a point A on the circle has coordinates (x,y) and another point B has coordinates (1,0) and that we know the angle θ between A and B. If θ is small, the the length of the straight line between A and B will be approximately equal to the length of the curve from A to B. So

Using trigonometry functions is cheating though. We want to see how the Ancient Greeks might have tried to calculate pi.

Using only square roots

Our challenge is to find the coordinates of point on the circle where we know is coordinates (x,y) and the angle θ is small, but not zero.

What we will do next find a sequence of points on the circle with coordinates $(x_0,y_0), (x_1, y_1), (x_2,y_2), \ldots $ where each point in the sequence is at half the angle to the previous one.

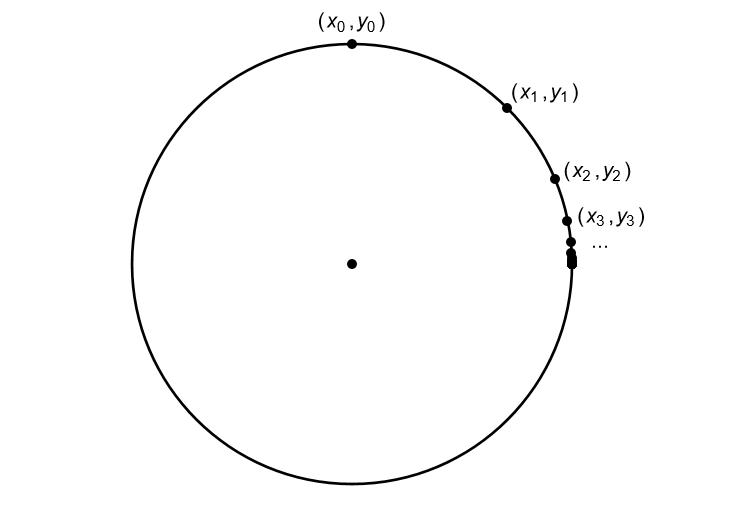
For the first point we will take $(x_0, y_0)$ to be the point $(0,1)$ which we know lies at an angle of 90 degrees to the horizontal. We will then be able to calcuate that $(x_1,y_1)$ is at an angle of 45 degrees, then that $(x_2,y_2)$ is at 22.5 degrees and so on.

All we have to do next is find a formula for the values of $x_{i+1}$ and $ y_{i+1}$ in terms of the previous point $(x_i,y_i)$.

For now let's cheat, and I will just tell you the formulae. We can work out why it is true later. Here are the formulae:

$$ x_{i+1} = \frac{y}{\sqrt{(1-x)^2 + y^2}} $$ $$ y_{i+1} = \frac{1-x}{\sqrt{(1-x)^2 + y^2}} $$

We can now write a table where we compute the coordinates of each point in turn using these formulae.

x-coordinate	y-coordinate	angle
$x_0=0$	$y_0=1$	90
$x_1=0.7071067811865475$	$y_1=0.7071067811865475$	$45.0$
$x_2=0.9238795325112867$	$y_2=0.3826834323650899$	$22.5$
$x_3=0.9807852804032304$	$y_3=0.19509032201612825$	$11.25$
$x_4=0.9951847266721969$	$y_4=0.09801714032956071$	$5.625$
$x_5=0.9987954562051724$	$y_5=0.04906767432741752$	$2.8125$
$x_6=0.9996988186962041$	$y_6=0.02454122852291228$	$1.40625$
$x_7=0.9999247018391445$	$y_7=0.012271538285723235$	$0.703125$

Assuming we can prove the formulae, we have shown how to compute pi using only mathematics! It is only an approximation, but the more terms you compute in the table, the more accurately you can compute pi, and if you use enough terms you can make the calculation as accurate as you like.

If you have never seen anything like this before, you have just made a big leap in your understanding of maths.

Proof of the half-angle formulae

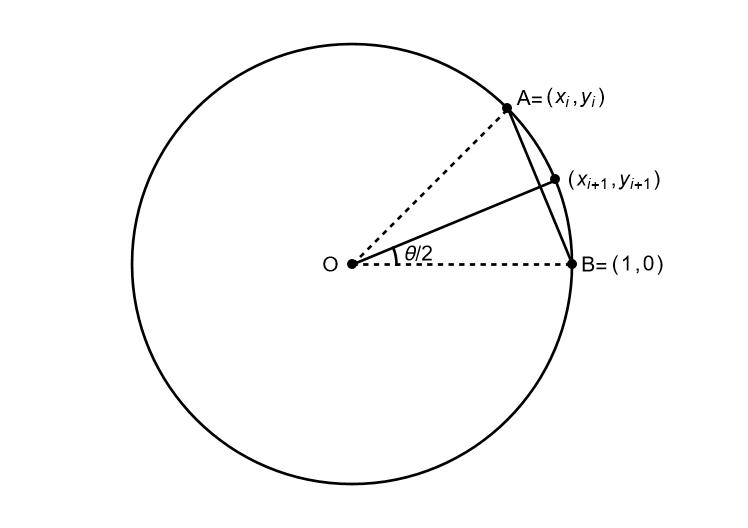
The gradient of the line $AB$ is given by $$\text{gradient AB} = \frac{\text{y-step}}{\text{x-step}} = \frac{y_i}{x_i-1}$$

The bisector of AOB is at right angles to the line AB so its gradient must be given by $$\text{gradient bisector}=-\frac{1}{\text{gradient AB}} = \frac{1-x_i}{y_i}$$ This is because, in general, if a line has gradient $m$, the line perpendicular to it has gradient $-\frac{1}{m}$.

Since we know the gradient of the bisector, we can say that every point $(X,Y)$ on the bisector must satisfy $$ Y = \left( \frac{1-x_i}{y_i} \right) X. $$ We also know by Pythagoras's Theorem that every point $(X,Y)$ on the circle satisfies $$ X^2 + Y^2 = 1. $$ The point $(x_{i+1},y_{i+1})$ lies on both the bisector and on the circle, so we must have these two equations $$ y_{i+1} = \left( \frac{1-x_i}{y_i} \right) x_{i+1}, $$ $$ x_{i+1}^2 + y_{i+1}^2 = 1. $$ Substitute the first equation into the second to get an equation for $x_{i+1}$: $$ x_{i+1}^2 + \left( \frac{1-x_i}{y_i} \right)^2 x_{i+1}^2 = 1. $$ Taking out the common factor we get $$ \left(1 + \left( \frac{1-x_i}{y_i} \right)^2 \right) x_{i+1}^2 = 1. $$ We can now solve for $x_{i+1}$ to get $$ x_{i+1} = \sqrt{ \frac{1}{1 + \left( \frac{1-x_i}{y_i} \right)^2 } }. $$ Here we notice that $x_{i+1}$ is positive, so it is correct to use the positive square root. We can simplify this to get the desired formula for $x_i$: $$ x_{i+1} = \frac{y_i}{\sqrt{(1-x_i)^2 + y_i^2}}.$$

Using the formula $y_{i+1} = \left( \frac{1-x_i}{y_i} \right) x_{i+1}$ we wrote down earlier we get the desired formula for $y_i$: $$ y_{i+1} = \frac{1-x_i}{\sqrt{(1-x_i)^2 + y_i^2}}. $$

And that completes the proof!